Statistical Graphics and more

Now that the world cup is over, and we finally have a winner, it is time to compare the expected values with the real outcome – don’t mix this up with comparing the outcome we would have liked to see with the real outcome, which is often done in business analytics …

The expected values are taken from Leitner, Zeileis and Hornik’s paper on the chances to win the world cup. What is appealing in their approach is to look at the bookmaker’s quotes rather than at the more long term scores from FIFA or ELO.

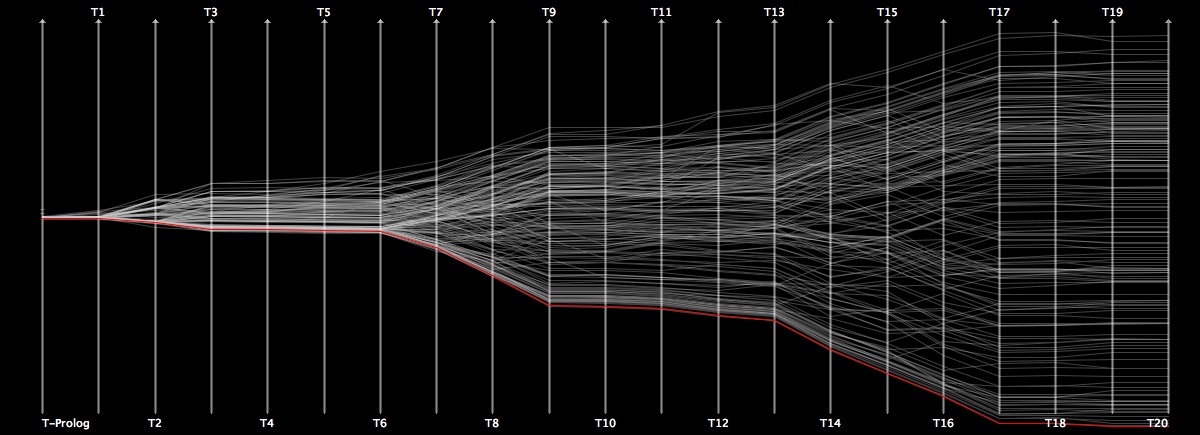
Here is a visualization ordered by the winning probabilities in %

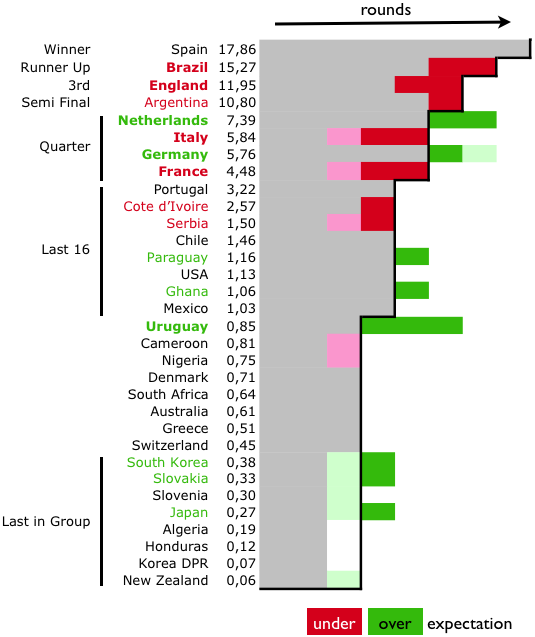
When being ordered by the winning probabilities, the team ranked 1st should win the cup, number two should be the loser in the final, and so on. During the group stage all teams perform 3 games, but we assume the 8 smallest ranks to be the last in their group.

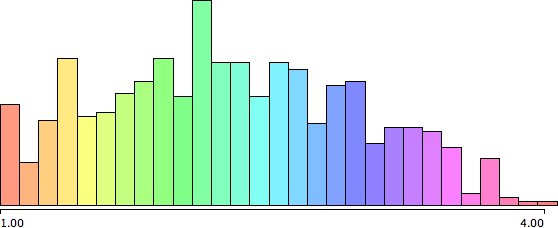
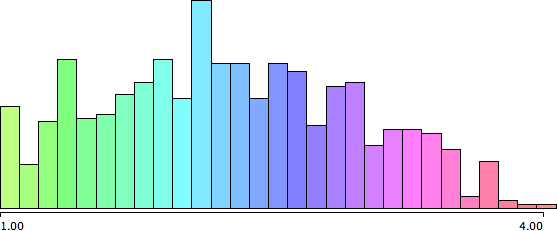
Given this ranking, we can visualize whether or not a team met the expectation or not. Teams falling short are indicated with red bars, i.e., stages they never reached, teams that performed above expectations extend with green bars.

What can we read from the graph? ITALY and FRANCE were the worst under-performer, as they did not only fall short of two stages, but they also ranked last within their groups. URUGUAY is clearly furthest above expectation as according to their rank, they were not even meant to advance to the last 16, but actually made it into the semi final.

What about SPAIN? Although they did win the cup, there was nothing really surprising given they were ranked 1st anyway.

Using the actual winning probabilities, we can also calculate what it actually took the teams to get to the point where they finally dropped out – that might probably rank them quite differently … but that will be another post.

July 3rd was probably the worst day to start the Tour de France, as many of us where captured by the quarter finals, which sent home nobody less than Diego Maradona’s dream team, which may dream for another four years now …

Although the world cup yet has to see its best matches, I will start to log the results in the usual ways as in 2005, 2006, 2007, 2008 and 2009. Contrary to the world cup, I swear not to give any model that predicts the winner …

Stage Results	cumulative Time	Ranks
(click on the images to enlarge) – each line corresponds to a rider – smaller numbers are shorter times, i.e. better ranks – all stages are on a common scale, – stage-results and cum-times are aligned at the median, which corresponds to the peloton

STAGE 2: QuickStep’s CHAVANEL takes the lead – did Fabian ran out of batteries 😉 ?
STAGE 3: CANCELLARA recharged; further spread of the field
STAGE 4: BOLE now last on a day without many changes
STAGE 5: Almost 75% of all riders roll in in the peloton
STAGE 6: GRABSCH “Loser of the day” – 9 drop outs by now
STAGE 7: CHAVANEL back at the top, with a newly sorted field after hitting the mountains
STAGE 8: ARMSTRONG falls behind
STAGE 9: ARMSTRONG gains some ranks on CONTADOR but the gap grows
STAGE 10: SCHLECK and CANCELLARA show quite opposite rank profiles
STAGE 11: LEIPHEIMER and CONTADOR the only “constant” top 10 riders
…
STAGE 14: Neither SCHLECK nor CONTADOR risk any kind of attack
STAGE 15: CONTADOR does not show fair play  and gets yellow only due to a technical defect of SCHLECK’s bike – but what would you expect with so many doping allegations on his account …
STAGE 16: ARMSTRONG still good for an extraordinary performance
STAGE 17: 26 drop outs – the rest will most probably make it to the Champs-Élysées
STAGE 18: Not the day of HERNANDEZ, but he knows how it feels to be last …
STAGE 19: GRABSCH and MENCHOV each get their 3rd place
STAGE 20: The profile of the winner, Alberto CONTADOR

See also the summary in this post

For those who want to play with the data. The graphs are created with Mondrian.

Although many of you might have seen this before somewhere on the web, I could not resist to post it as I used two of the effects in my visualization courses.

As you can see, context is always key for a right interpretation … Enjoy!

Peter Huber referred to “the rawness of raw data”, a kind of data we would not expect to find in a textbook. The book of Fahrmeir and Tutz on multivariate modelling refers to the visual impairment data from Liang et al., 1992 in table 3.12:

Visual Impairment Data from Liang et al. as found in Fahrmeir and Tutz

Nothing wrong here at first sight; but how would you tell? There are some people who are actually able to look at non-trivial table data and spot “the round peg in the square hole”, but that just won’t work for the rest of us.

As you might guess, I am going to make a case for graphics here.

Let’s start with what the mainstream would do: plot the data in a dotplot like thing using the trellis paradigm of conditioning. I used ggplot2 to make sure to trellis state-of-the-art. A simple

  qplot(count, side, data=visual2, colour=impaired) + facet_grid(age ~ race)

gives me:

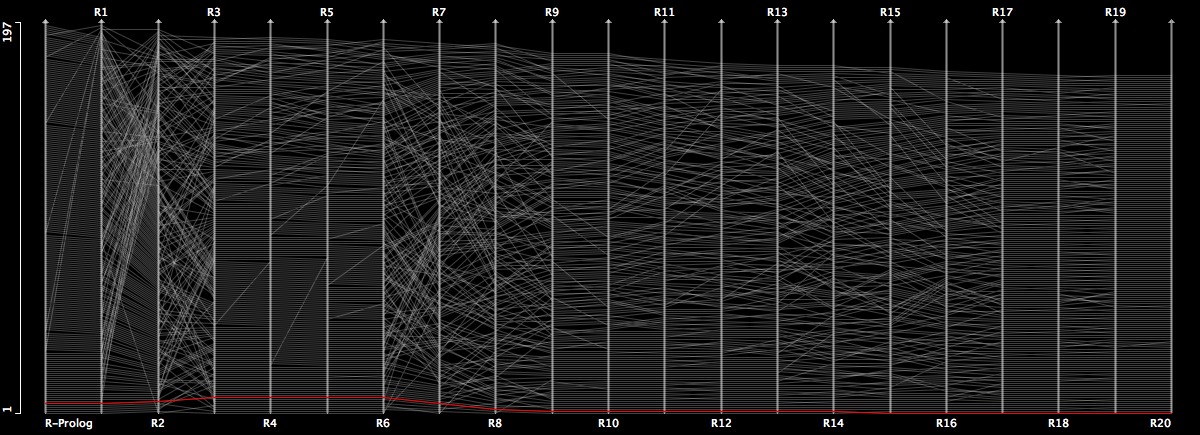
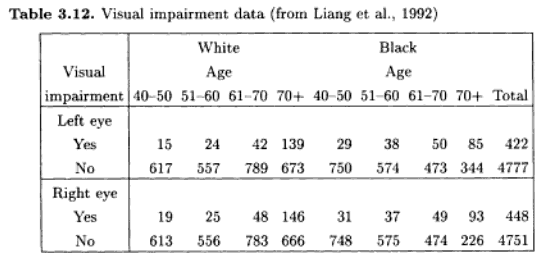
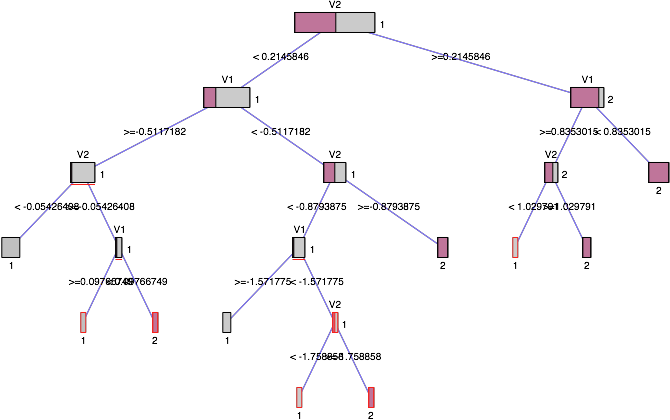
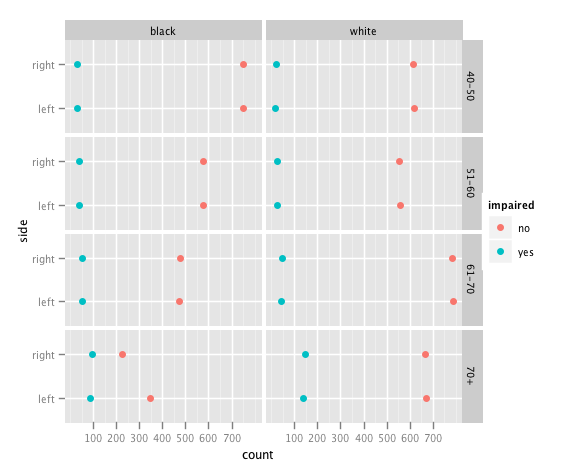(I still have a hard time to find that syntax intuitive …) Surprisingly this plot already is sufficient to spot the “problem” in the data, although some important properties of the data can’t be seen here.

A mosaic plot makes the whole thing even easier:

(impairment cases highlighted, left and right is left and right)

The left and right cases are (what a surprise) always of the same size, except for the 70+, black – hard to believe that in this group 110 cyclops show up not having a right eye.

In the mosaic plot the higher proportion of the impaired right eyes for 70+ blacks jumps immediately to ones eyes, but what reveals the error is the missing independence between race and side for 70+. That implies that we have too few cases here, and what is ‘226’ in the table should actually be ‘336’.

Here is the (corrected) data.

There are certainly many models, which try to “calculate” which team will win the 2010 soccer world cup. Looking at the teams that already dropped out, the range of models which were obviously not predicting correctly gets quite big. Here is a visualization of my favorite:

For those of you, who more believe in numbers and don’t want to be fooled by visual explanations, the years in which the (multiple) cup winners succeeded all add up to 3,964. Like for all good models, we have outliers, i.e., two of the outcomes do not fit the model, which – hey- is 2 out of 15 = 13% error.

Most importantly though, a good model predicts the things we believe in. All over all, I think the model fulfills all good practices of classical statistics. The only thing that makes me think a bit are the team to beat to get to the prediction: Argentina, Spain, Brazil.

Anyway, good to have a second “evidence” apart from the octopus.

Update: I did this in Apple’s Keynote, as I was to lazy to give protovis a try – anyone more ambitious?

Color brushing (i.e., the persistent assignment of colors to cases) was one of the most requested and most ignored (on my side) features for Mondrian. I gave in at some point and ever since I get the never ending complaint over using “the wrong” colors – which I now ignore for the most part as n users will have n different preferred color schemes.

Nonetheless, there is the continuous color scale which usually utilizes some sort of rainbow color scheme in order to differentiate between a maximum of hues. The whole thing seem to be pretty easy to implement in HSB color space. Once you decided on some reasonable S and B you only need to go round in the H circle and you are done. Here is what you get:

Looks pretty neat, but has two obvious problems:

• If you use the complete circle, you won’t be able to distinguish between the values at the edges, as they are actually the same
• If you use a background color (light yellow for Mondrian) you should avoid this color altogether.

The possible solution solves both problems at once. The first problem needs to avoid a certain color range such that “minimum color” and “maximum color” are far enough apart. For Mondrian, this is certainly the yellow range; which solves the second problem. This is what the update looks like:

No spectacular change, but this is actually the solution which I should have thought of in the first place.

It did start with only three players and the keeper on the board, which I used to explain my kids (first graders and below) what offside means, and their creativity expanded it to what looks like Joachim Löw’s strategy for the Ghana match next Wednesday:

Let’s proceed with fingers crossed!

(The strategy on the board shows no shots on the goal, so I hope Löw’s drawings look differently 😉 )

I never thought I would ever embed videos from FOX on my blog, but this one needs to be covered:

Watch SPSS co-founder Norman Nie talking about the “… unbelievably powerful open source language called R …” and “… I am not sure that SPSS is our biggest competitor there is an even larger competitor out there called SAS …”

Good luck on this mission!

Special times fuel the development in specific areas. E.g., during WWII a lot of (sometimes curios) inventions and technical optimizations came up – usually not supporting humanity. The Soccer World Cup seems to spur the development of soccer visualizations and sports visualizations in general. My favorite (and apparently not only mine) one is this overview:

Querying places, teams, groups and dates highlights all associated information in the other dimensions. Selecting the “marginal distributions” (at the arrows) shows calendars, match schedules and maps – neat!

Infosthetics lists some more visualizations which even show live updated soccer statistics. Although I don’t believe much in this kind of statistics like – every game on a Sunday when Lionel Messi was wearing blue socks was won by Argentina with one goal by Messi – I guess it is fun to watch the live updating of the objective soccer statistics and comparing it to the subjective observation of the game and trying to find out how this matches up and probably might explain why a team wins or not.

Enjoy the World Cup!

R did definitely not start to be THE statistical computing tool. The “two Rs” in far down-under just needed some tool which was not too expensive and structured enough to support the elementary statistics classes filled with hundreds of students. Another constraint was the computing lab which was large enough, but “only” filled with Mac IIs.

As the “two Rs” were computer savvy and knew the S-language, they started with a simple copy of the basic functionality of the S-language. Everything else which happened since the early 90s is history by now.

There are quite a few tools and languages which managed to set fundamental standards like Postscript, pdf, LaTeX, Java, etc. but, e.g., C++ didn’t offer inline Java or the formula editor in Word did not get a LaTeX compatible mode.
Not so for R.

Sample session which uses the R-interface to the Oracle Data Mining functions

The list of applications which connect to R and support the utilization of R functions in some way is quite long already, and seems to get new prominent members every now and then:

• SAS
  allows using R-code within IML (despite the initially quite aggressive take on R)
• SPSS
  supports writing R code for several versions now
• Statistica
  has R integration
• JMP
  uses the power of R
• Oracle
  just released their own R package R-ODM to use Oracle data mining functions from within R.
• …

Certainly, with Rserve it is more or less a piece of cake to talk to R for anyone who knows the basics of programming, but companies like SAS and Oracle are quite big players, who usually care a xxxx about what other projects and/or standards do.

In some sense it looks like the Goliaths start to surrender to the David, although he never really attacked …

Tree layouts are not too uncommon in statistics. CART is build upon tree hierarchies and random forrest uses these trees extensively. Area based plots like barcharts or histograms are also well understood by most statisticians. But when it comes to joining the two concepts – which will yield treemaps – many statisticians get somewhat lost. The reason is somehow related to that fact that concurrent concepts like mosaic plots and trellis displays aka lattice graphics seem to get mixed up.
There will be a series of three posts on the three concepts from which this is the first one on

Tree Maps:

In short, a treemap is nothing else than an alternative display of a tree hierarchy. The primary reference to treemaps goes back to Ben Shneiderman’s technical report. Whereas the classical tree usually “just” shows the hierarchy, a treemap usually also encodes a quantitative attribute which is attached to the leaf nodes (and add up to the root of the tree).

Here is an example of a classification tree

This tree has 10 terminal nodes, and each node has a size proportional to the number of cases, which fall into this category. The corresponding treemap looks like this:

Note that in this tree all splits are binary, which means that in the corresponding treemap the splits always alternate between vertical and horizontal.

Squarified Tree Maps:

When treemaps are used to visualize a recursive partitioning, the number of splits and terminal nodes will be relatively small. But with arbitrary hierarchies, we will end up with potentially very many splits and/or terminal nodes. As splits on the same level will be split along the same direction, aspect ratios will get extreme. The following sketch shows the problem for 7 terminal nodes of size 6, 6, 4, 3, 2, 2, 1.

Thus we need some way to distinguish between “real” splits, which define hierarchies, and “convenience” splits, which are used to improve the aspect ratios of the tiles.

Cushioned Tree Maps:

One way to achieve this distinction would be to use thicker lines for “real” splits. The more popular version is to use so called cushioned treemaps. Here is an example, depicting parts of a file system (actually the files of my talks since 1994):

Looks pretty fancy, but does only partly cure the problem.

The bottom line is that if you ever have a hard time to understand a treemap, it is most probably due to the fact of squarification, which does not properly distinguish between hierarchy splits and squarification splits.

It was at the 1997 JSM in Anaheim, CA, when I peeked into one of the seminar rooms, and found the continuing presentation of the ASA graphics video library. Although, most of the movies are not really new, they are still very inspiring and interesting to watch.

One of my favorites is Bill Eddy’s air traffic movie, which is now 15 years old.

The vulcano eruption that filled the European skies with ashes and halted essentially all air traffic flying into or out of European airports inspired the visualization by Ito listed on infosthetics.

(Airspace Rebooted from ItoWorld on Vimeo)

Todays visualization tools and improved hardware make the new movie far more attractive – but it is essentially the same visualization Bill Eddy showed 15 years ago.